Vector Swarm

This experiment was done in 2005 in New York. It was exposed on a metal stage using a brief flash exposure. In this experimental setup, there is an NdFeB permanent magnet a few centimeters below and to the right of the swarm of tracks. The magnetic field lines of the magnet in no way correspond to the tracks. That is, the tracks do not follow the field lines and the observed multiple concentric circle pattern centers (shown below) are several centimeters from the magnet.

Fig. 0 - The actual location of the NdFeB magnet in the exposure.

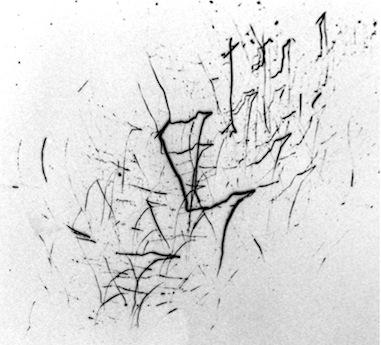
Fig. 1 - 'Vector Swarm.'

Our tracks from Fig. 1 are correlated as a group but cannot all be overlaid on top of each other. These tracks appear to be correlated, yet twisted or acted upon by some central force. The tracks were digitized in a vector graphics editor and shown in Fig. 2.

Fig. 2 - 24 of the highly visible tracks from Fig. 1 were digitized point-by-point in a graphics editor.

A perpendicular was dropped from each corresponding segment and the center was estimated as the intersection of all perpendiculars. For now, to get an idea of the behavior, we roughly approximate the curvature using concentric circles drawn from the point of intersection of the perpendiculars.

Corresponding track segments were labeled as in Fig. 3.

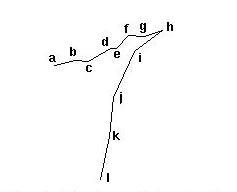
Fig. 3 - Legend of labeled vertexes for prototype track.

Tracks were plotted and perpendiculars drawn from each segment showing the geometric centers as in Fig. 4 and Fig. 5.

Measurements taken at successive common points of corresponding tracks indicate a swarm of identical particles each going through coordinated abrupt transitions at each vertex or kink. The field influence on corresponding track segments are geometric centers.

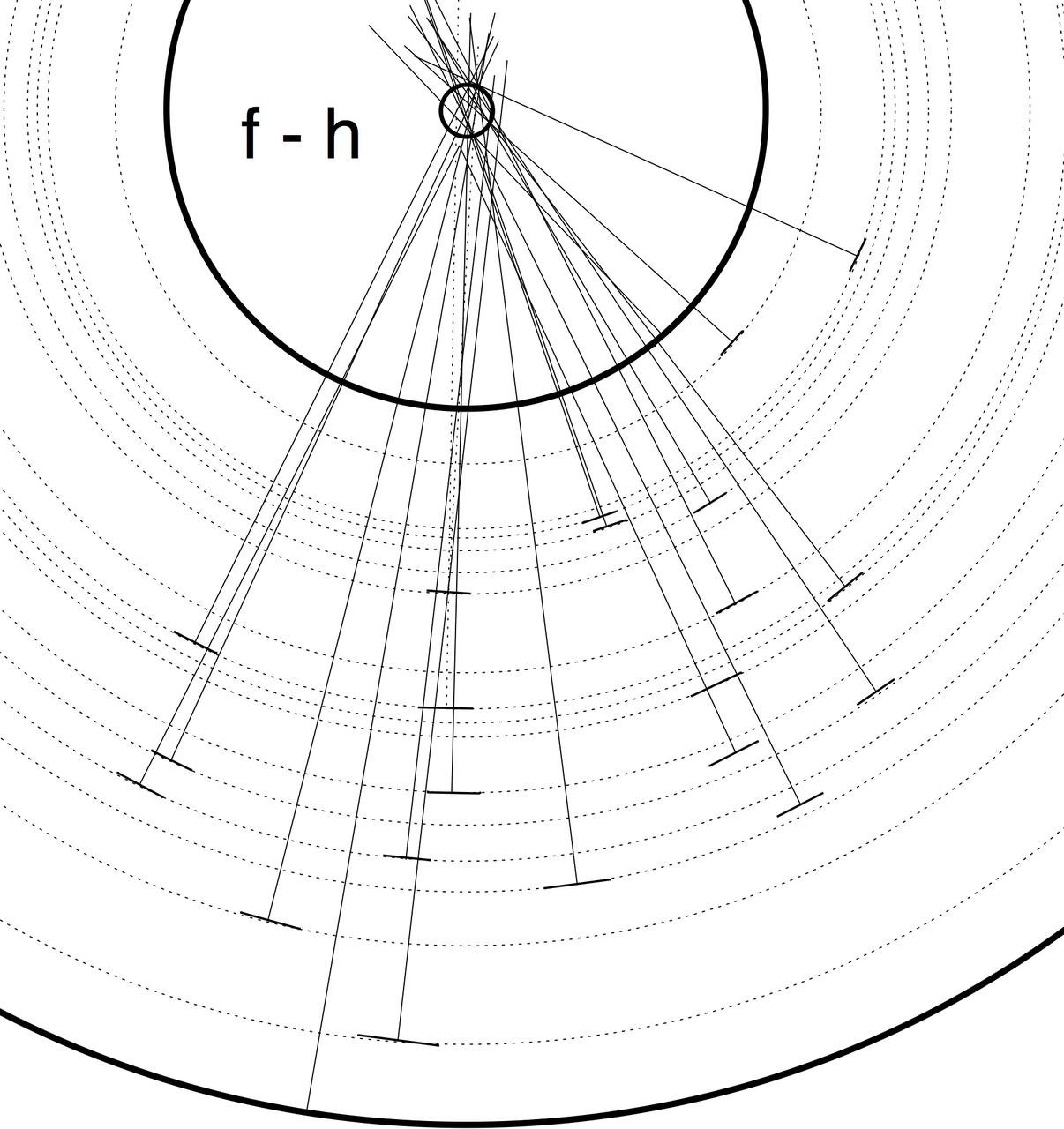
Fig. 4 - Plot of segments f-h showing the geometric center of line segments extracted from Fig. 1. Segment numbering corresponds to Fig. 3.

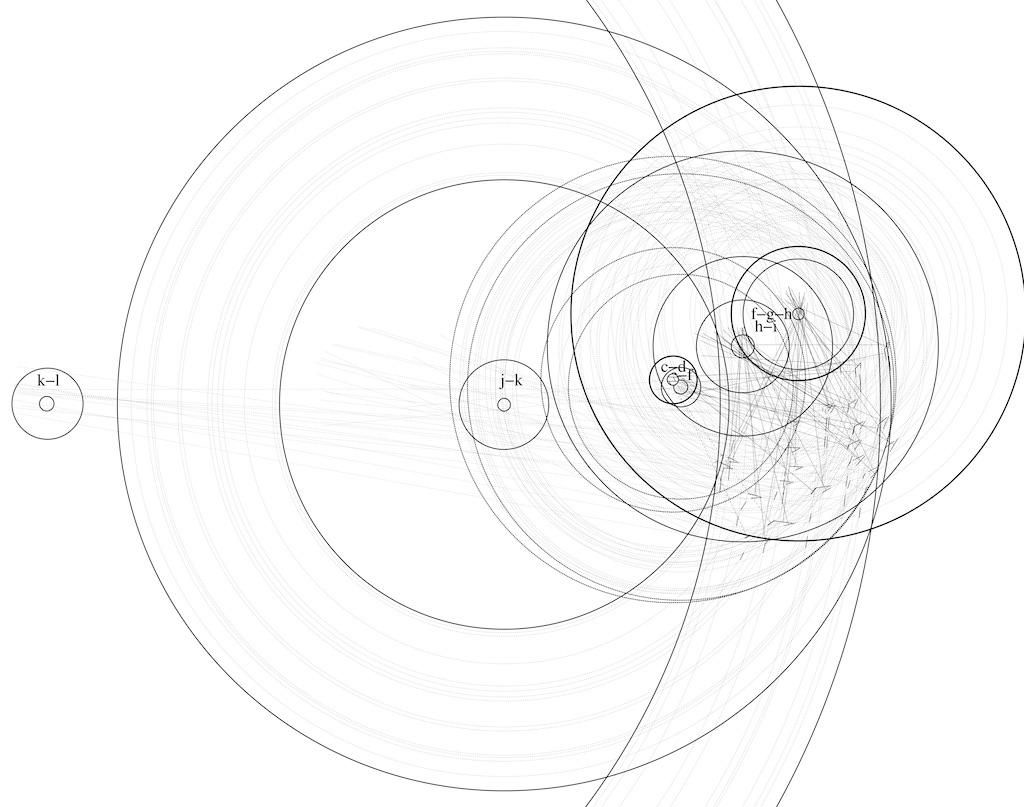
Fig. 5 - Plots of geometric center were superimposed upon each other in exact coordinates. The further the point-like geometric center is from the vertex h, the bigger the concentric circles become.

Fig. 4 shows a plot of the geometric center for measurable segments f-h in the correlated group from Fig. 1 and Fig. 2. Fig. 5 shows the combined plots of all geometric centers.

New Vector Swarm

This exposure was done in 2014 in Norway. The experimental setup for this exposure was simple. It was just a 4x5 sheet of film on a cardboard stage exposed by 2 LEDs. No applied electric or magnetic field.

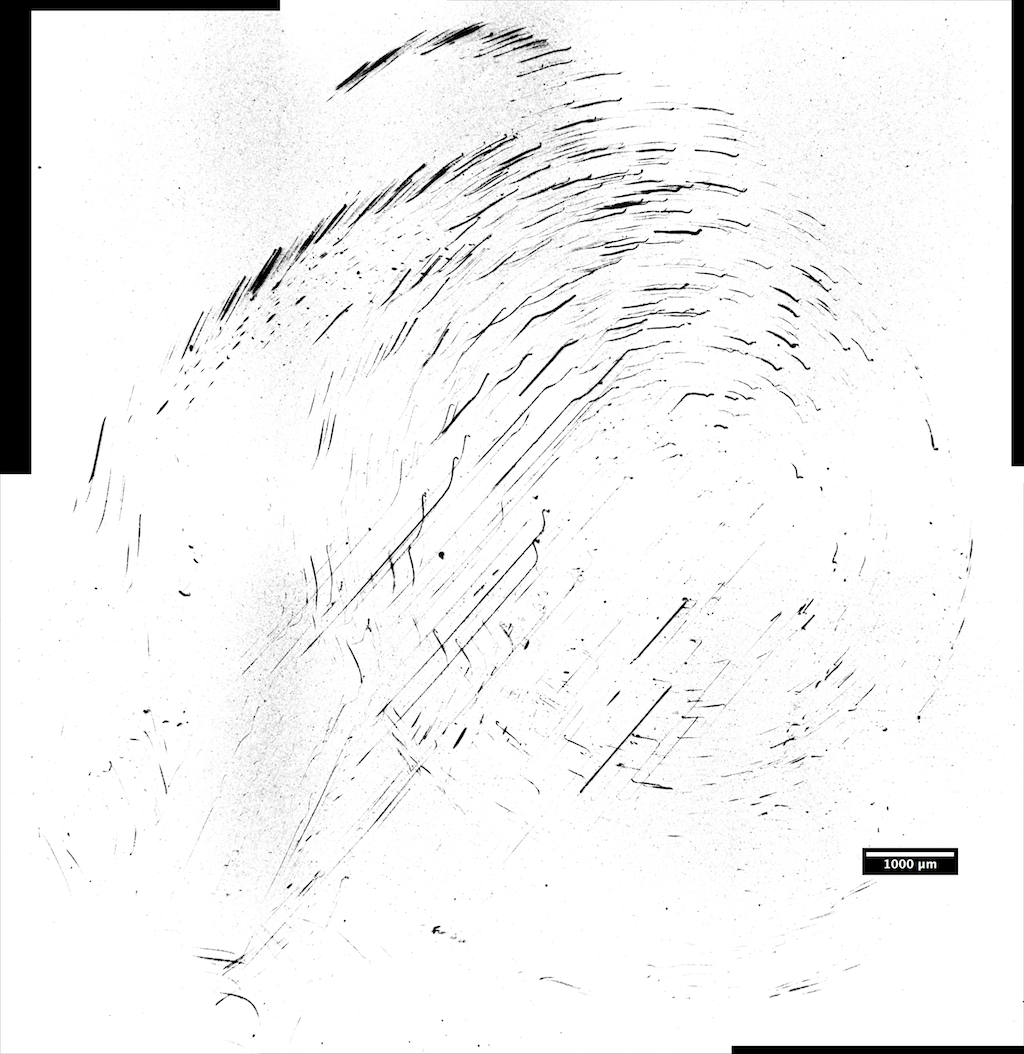
Fig. 6 - Exposure showing concentric circle pattern of tracks.

Fig. 7 - Annotated image with perpendiculars from tracks and concentric nearly circular ellipses.

This exposure clearly shows the presence of a point-like central force. Now what does the central force need to be for certain types of particles to form such a pattern?

[1] Possible detection of tachyon monopoles in photographic emulsions,

Engineering Physics (No. 6), 15-45 (2013).